Process of Discrete Wavelet Transform (I): Wavelet Decomposition

Wavelet decomposition is to decompose a signal into approximation and detail coefficients

The Process of Discrete Wavelet Transform will be divided into three Parts:

Part I: Wavelet Decomposition

Part II: Wavelet Reconstruction

Part III: Wavelet Partial Reconstruction

In previous posts, we have talked about some basic concepts of wavelets transform and wavelets transform classifications. Understanding the whole process of Discrete Wavelet Transform (DWT) is essential before applying it into real-world cases. This post will introduce you to the general decomposition process of DWT, including single-level decomposition, and multi-level decomposition.

Table of Contents

1. Wavelet Decomposition

The process of using the discrete wavelet transforms (DWT) to decompose a signal or an image into approximation and detail coefficients at different levels is called wavelet decomposition or analysis.

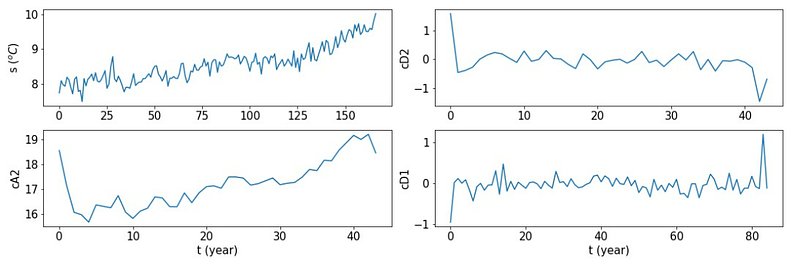
For example, a temperature signal (s) is decomposed into two levels, where cA2 is the approximation coefficient at the level of two, cD2 and cD1 are the detail coefficients at the level of two and level one, respectively.

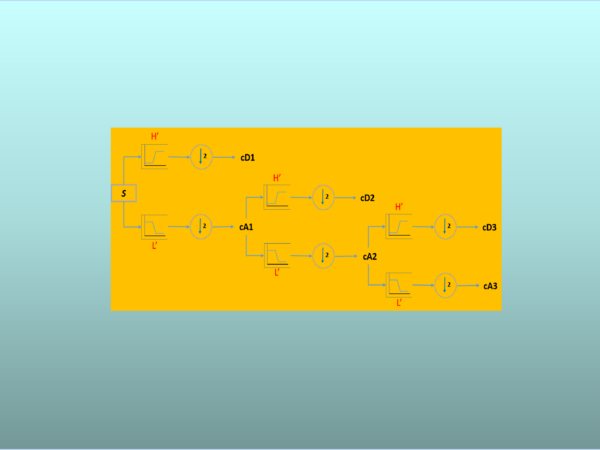
In general, there are single-level decomposition and multi-level decomposition.

2. Single-level decomposition

Single-level decomposition is also called one stage decomposition. We can understand the process in two steps.

(1) Pass through two filters

We already discussed basic concepts of filter method and visualization of filter banks in one previous post. Filter method is an efficient way to implement DWT in practice.

The original signal (S) is decomposed into two signals, A and D after passing through two complementary filters, hightpass (H’) and lowpass (L’). A is the low-frequency content, usually called approximation, is the most important part of a signal, which is the identity of a signal. D is the high-frequency content, often called details, which imparts flavor or nuance.

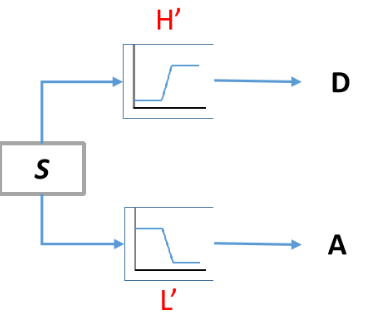
However, the problem is that this operation will generate twice as much data as the original.

(2) Downsampling

We keep only one point out of two in each of the two newly decomposed signals to get the complete information, and this process is the notion of downsampling. Through this process, it produces two sequences cA and cD, called approximation and details coefficients, i.e. DWT coefficients.

3. Multi-level Decomposition

In most cases, one stage decomposition cannot meet our need, and thus we need multi-level decomposition to a signal.

(1) Decomposition Process

The decomposition process will be iterated, with successive approximations being further decomposed in turn.

Since the analysis process is iterative, in theory it can be continued indefinitely until the individual details include only a single sample or pixel. In practice, however, we’ll select a suitable number of levels based on the nature of the signal and our goal.

(2) Wavelet Decomposition Tree

One signal is broken down into many lower resolution components after multiple level decomposition. This process is usually called the wavelet decomposition tree, since it looks like a tree.

If you like this post or think it is helpful, please do not forget to give a clap to show your kind support. I appreciate it for your support! Your support is the best encouragement for me to produce more helpful products.