Learning Wavelet Transform should start from basic concepts
I published three posts at the very beginning when I started my blogs, which are about visualization of wavelet function and scaling function, visualization of filter bank of a Discrete Wavelet and applications of wavelet transform.
From this post, I will continue to write some practical tutorial articles on how to apply Wavelet Transform to solve real-world problems. It is better to know some basic concepts related with Wavelet Transform (WT) before using it for real-world cases.
1. What is a Wavelet?
A wavelet is a wave-like oscillation, which is a “brief oscillation” or “small oscillation”. Its amplitude begins at zero, increases or decreases, and then returns to zero one or more times. Let’s see some wavelets plots as follows:

2. Wavelet Transform
In the signal processing context, Wavelet transform (WT), also called wavelet analysis, is a method to decompose an input signal of interest into a set of elementary waveforms, i.e. “wavelets”
WT provides a way to analyze the signal by examining the coefficients (or weights) of these wavelets. It is probably the most recent solution to overcome the shortcomings of the Fourier transform.
(1) Two basic factors
- scale (or dilation): Stretched or compressed (or shrunk) wavelet
- shift (or location): the positions of the wavelet
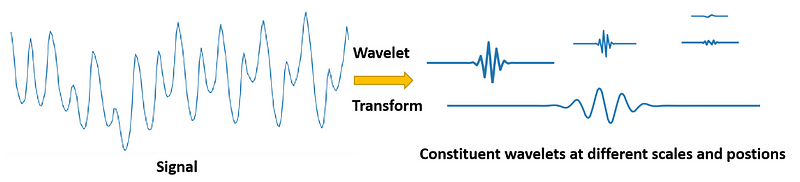
WT uses inner products to compare the similarity between a signal and the wavelet at various scales and positions, i.e. shifted and compressed and stretched versions of a wavelet, to obtain the wavelet coefficients.
(2) Scale and frequency
The general correspondence between scale and frequency is:
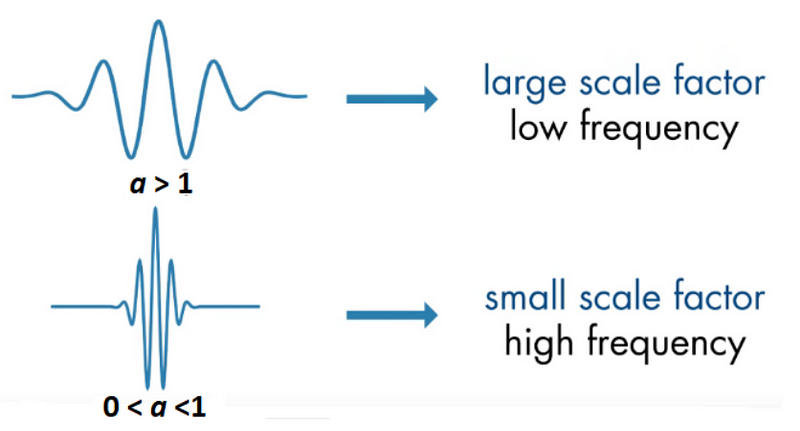
- Small scale a ⇒ Compressed wavelet ⇒ Rapidly changing details ⇒ High frequency ω.
- Long scale a ⇒ Stretched wavelet ⇒ Slowly changing, coarse features ⇒ Low frequency ω.
3. Signal and Time Series
Since WT is a method to deal with an input signal of interest, then what a signal and what different between a signal and a time series.
(1) A signal
- It is more related to physics, image analysis, engineering / science domains
- Many signals are basically a time series once they are sampled at a certain time interval, such as speech, audio, power, water and environmental quality data from sensors or labs, etc.
- A signal is more general, not necessary measured by time, maybe spatial coordinates, distances to a source, or multidimensional
- Almost anything carrying information can be interpreted as a signal.
(2) Time series
- It is more related to data analysis domain
- Any data points are varied and measured over times, bank interests change, GDP growth, COD changes in river, population growth, etc.
- It usually depicts the data values (y) is a function of time (t): ????=????(????)
- A time series is always indexed by time
In this sense, a time series is a signal varied and measured over times. Then it is not hard to understand why WT is usually applied in time series analysis.
4. Signal and Wave
From the above, we know that a signal is a more general and abstract concept, which is almost anything carrying information. A signal has no physical manifestation.
Whereas, a wave is a physical phenomenon, which can be used to transmit signals. Thus, we see a wave as a wave signal. A wave can be modelled and measured.
- Period (????): refers to the time taken to complete one oscillation, i.e. cycle from one peak to the next (or from any point to the next matching point),
- Amplitude (????): the height from the center line to the peak (or to the trough).
- Frequency (????): the number of oscillations per unit time
Besides, a wave has length, called wavelength, which is the distance over which a wave repeats, which can be defined as the distance between two successive crests or troughs of a wave.
In addition, waves typically has different forms, called waveform, which describes the shape or form of a wave signal. There are four basic types of waveform, such as
- Sine wave
- Square wave
- Triangle wave
- Sawtooth wave
5. Online courses
If you are interested in learning how to apply wavelet transform to real-world cases with Python step by step, you are welcome to enroll my courses:
(1) Very basic one
Practical Python Wavelet Transforms (I): Fundamentals
(2) For Real-world projects
Practical Python Wavelet Transforms (II): 1D DWT