Differences, Advantages and Disadvantages of DWT and UWT
In this article, we will review generally the differences between the Decimated Wavelet Transform (DWT) and the Undecimated Wavelet Transform (UWT) or the Stationary Wavelet Transform (SWT).
In general, the Undecimated Wavelet Transform (UWT), also known as the Stationary Wavelet Transform (SWT), is a variant of the traditional Decimated Wavelet Transform (DWT). While the DWT downsamples the signal at each level of decomposition, the SWT overcomes this limitation by maintaining the original signal length throughout the analysis. This shift-invariant wavelet transform offers several advantages over the DWT, including improved frequency localization and shift-invariance. In this way, the SWT provides a powerful tool for signal and image processing tasks, such as denoising, feature extraction, and time-frequency analysis.
1. Decimated Watelet Transform
The Decimated Wavelet Transform (DWT) is a widely used technique in signal and image processing for analyzing and decomposing signals into different frequency components. Unlike the Continuous Wavelet Transform (CWT), which provides a continuous-time representation of the signal, the DWT operates on discrete-time signals and performs a multi-resolution analysis.
The DWT involves a series of filtering and downsampling operations to decompose a signal into different frequency bands or scales. It involves to remove, drop a large percentage or part of the signal, and it suffers a drawback that is not a time- invariant transform. Thus, the DWT of a translated version of a signal S is not, in general, the translated version of the DWT of S.
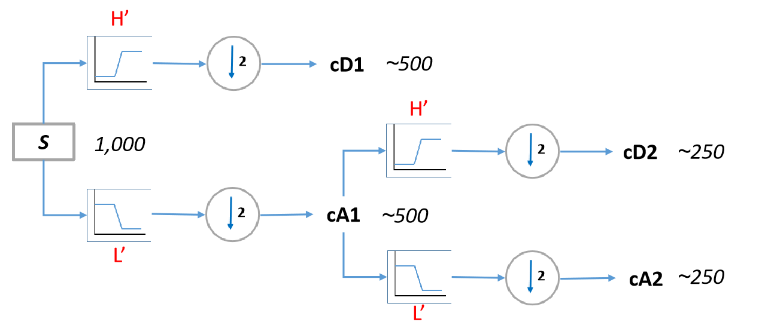
The DWT provides a multi-resolution representation of the signal, with different levels or scales capturing different frequency bands. The high-frequency components represent fine details, while the low-frequency components capture the coarse information. The DWT allows for efficient representation and analysis of signals in both time and frequency domains.
The choice of wavelet function plays a crucial role in the DWT. Different wavelets have different frequency characteristics and properties, making them suitable for specific types of signals or analysis goals. Commonly used wavelets include Daubechies, Symlets, and Haar wavelets.
The DWT has various applications, including signal denoising, compression, feature extraction, image processing, and time series analysis. It provides a powerful tool for analyzing and understanding the frequency content of signals in a multi-resolution framework.
2. Undecimated Watelet Transform
The Undecimated (or Nondecimated) Wavelet Transform (also known as the Stationary Wavelet Transform or SWT) is a variation of the traditional Decimated Wavelet Transform (DWT) that overcomes some of its limitations. While the DWT involves downsampling the signal at each level of decomposition, the SWT avoids this downsampling, resulting in a shift-invariant wavelet transform that preserves the original signal length throughout the analysis.
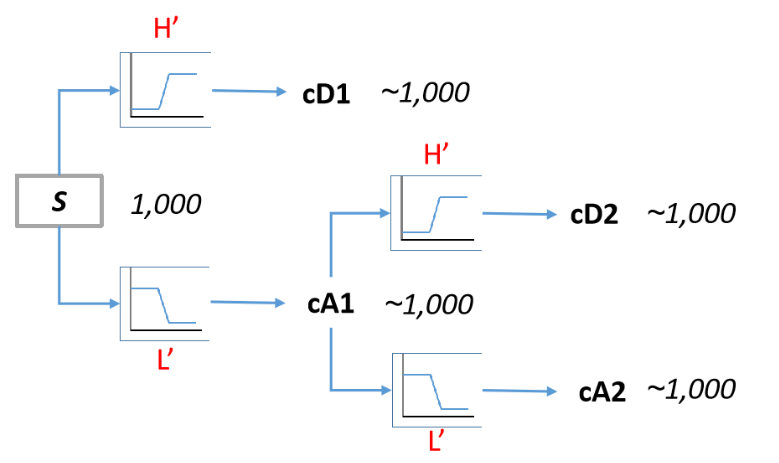
The Undecimated Wavelet Transform provides several advantages over the DWT:
Shift-Invariance: The SWT is shift-invariant, meaning that small shifts in the input signal result in small shifts in the transform coefficients. This property is beneficial for applications such as signal denoising and time series analysis.
Redundancy: The SWT has a redundancy factor of 2, which means that the number of coefficients in the transformed signal is doubled compared to the original signal. This redundancy can provide more accurate representation of signals with localized features. Improved Frequency Localization: The SWT has improved frequency localization compared to the DWT, especially for high-frequency components. This is because the SWT avoids aliasing caused by downsampling.
The choice of wavelet function is still important in the Undecimated Wavelet Transform. Different wavelets have different characteristics and are suitable for different types of signals or applications.
The Undecimated Wavelet Transform is commonly used in various applications, including signal and image denoising, feature extraction, time-frequency analysis, and biomedical signal processing.
It’s worth noting that the SWT can have higher computational complexity compared to the DWT due to the absence of downsampling. However, this drawback is often mitigated by the benefits it offers, especially in applications that require shift-invariance or precise localization of high-frequency components.
Conclusion
The Undecimated Wavelet Transform (SWT/UWT) has emerged as a valuable technique in the field of signal and image processing. By avoiding downsampling and maintaining the original signal length, the SWT provides shift-invariant analysis and improved frequency localization. These advantages make it a suitable choice for applications that require precise representation and analysis of signals, especially in cases where small shifts in the input signal need to be accurately captured. From denoising to feature extraction and time-frequency analysis, the SWT has found widespread applications and continues to be an area of active research. By harnessing the power of wavelet analysis, the SWT enables researchers and practitioners to delve into the frequency domain and extract meaningful information from complex signals and images, contributing to advancements in various domains, including biomedical signal processing, audio and video processing, and more.
Originally published at https://medium.com/ on June 26, 2023.