1D Discrete Stationary Wavelet Transform (II): Maximum Decomposition Level

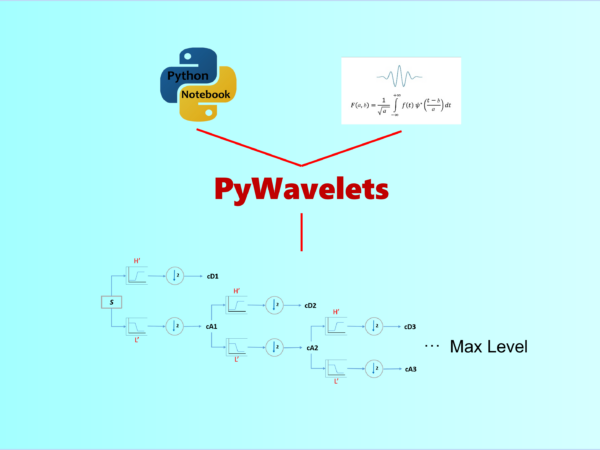
PyWavelets provides an easy method to calculate the maximum level of Stationary Wavelet Transform (SWT)

In the previous article, we have talked about how to decompose 1D signal using Stationary Wavelet Transform (SWT). The maximum decomposition level in the Stationary Wavelet Transform (SWT) depends on the length of the input signal. It is determined by the number of times the signal can be downsampled by 2 until it reaches a length of 1 or less.

The information of maximum decomposition level is valuable as it helps in setting the appropriate number of decomposition levels for a signal analysis task. It allows us to determine the number of approximation and detail coefficients that will be generated at each level, providing insights into the signal’s frequency content and capturing various scales of detail.

Understanding the maximum decomposition level aids in selecting an optimal balance between capturing fine details and avoiding excessive decomposition, which could lead to noise amplification or computational overhead. By leveraging the capabilities of PyWavelets and the concept of the maximum decomposition level, researchers, and practitioners can effectively utilize SWT for applications such as signal denoising, feature extraction, and time-frequency analysis, among others.

3.1 Method

We can easily calculates the maximum level of SWT for data of given length using the following function in PyWavelets.

pywt.swt_max_level(input_len)

Parameters:

• input_len [int] Input data length

Returns:

• max_level [int] Maximum level of Stationary Wavelet Transform for data of given length

3.2 An example

Let’s illustrate this with a simple example using the PyWavelets library in Python.

import pywt

S = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]

# Get the maximum decomposition level
max_level = pywt.swt_max_level(len(S))

print("Maximum decomposition level:", max_level)

Maximum decomposition level: 4

In this example, we have an input signal with 16 samples. We use the pywt.swt_max_level function to determine the maximum decomposition level based on the length of the signal. In this case, the maximum decomposition level for the input signal of length 16 is 4. This means that the signal can be decomposed into 4 levels, resulting in 4 sets of approximation and detail coefficients.

Let’s decompose it into the maximum level with ‘db2’, which refers to the Daubechies 2 wavelet.

coeffs = pywt.swt(S, 'db2', level=4)
coeffs

[(array([34., 34., 34., 34., 34., 34., 34., 34., 34., 34., 34., 34., 34.,
34., 34., 34.]),
array([ -5. , 0.56217783, 5.02627944, 8.75833025,
12.12435565, 13.75833025, 14.02627944, 11.56217783,
5. , -0.56217783, -5.02627944, -8.75833025,
-12.12435565, -13.75833025, -14.02627944, -11.56217783])),
(array([27.57716447, 23.64411081, 20.48751428, 17.84855585, 15.46841646,
14.31302194, 14.12355325, 15.86593621, 20.50609665, 24.43915031,
27.59574684, 30.23470527, 32.61484466, 33.77023918, 33.95970787,
32.21732491]),
array([ -8.5732141 , -6.76148078, -5.01909782, -3.79435295,
-3.53553391, -2.56960808, -1.34486321, 1.81173332,
8.5732141 , 12.69573645, 14.81705679, 12.55703574,
3.53553391, -3.36464759, -8.45309576, -10.57441611])),
(array([18.19615242, 12. , 7.53589838, 5.80384758, 7.80384758,
9.80384758, 11.80384758, 13.80384758, 15.80384758, 17.80384758,
19.53589838, 22. , 26.19615242, 28.39230485, 29.12435565,
26.39230485]),
array([-4.92820323e+00, -2.73205081e+00, -1.00000000e+00, 7.21644966e-16,
-5.55111512e-17, -2.22044605e-16, 9.99200722e-16, 1.11022302e-15,
-1.77635684e-15, -6.66133815e-16, -1.00000000e+00, 7.32050808e-01,
8.92820323e+00, 9.66025404e+00, -2.00000000e+00, -7.66025404e+00])),
(array([ 8.62398208, 2.31078903, 3.7250026 , 5.13921616, 6.55342972,
7.96764328, 9.38185685, 10.79607041, 12.21028397, 13.62449753,
15.0387111 , 16.45292466, 17.86713822, 19.28135178, 22.76611771,
20.59402938]),
array([-2.07055236e+00, 1.66533454e-16, 1.11022302e-16, 3.33066907e-16,
4.44089210e-16, 2.22044605e-16, 0.00000000e+00, 2.22044605e-16,
1.33226763e-15, 4.44089210e-16, 8.88178420e-16, 8.88178420e-16,
4.44089210e-16, 4.44089210e-16, 7.72740661e+00, -5.65685425e+00]))]

Next, let’s see how it is going if we decompose the signal into levels more than its maximum levels., say 5 in the example.

coeffs = pywt.swt(S, 'db2', level=5)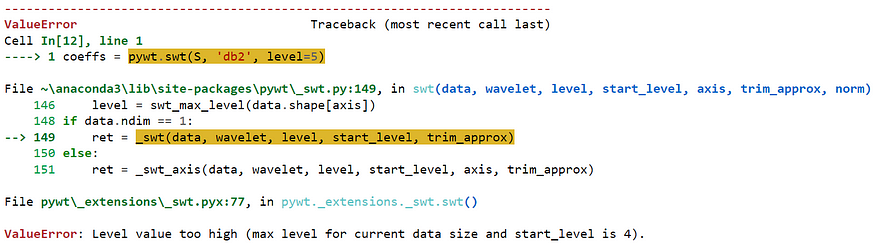

There will be an error if we try to decompose the signal more than the maximum level.

Conclusion

The determination of the maximum decomposition level in the Stationary Wavelet Transform (SWT) using PyWavelets allows us to understand the depth to which a given signal can be decomposed. By analyzing the length of the input signal, we can determine the maximum level of decomposition.

In our example, we used the PyWavelets library in Python to calculate the maximum decomposition level for a simple input signal of length 16. By applying the pywt.swt_max_level function with the appropriate parameters, we obtained a maximum decomposition level of 4.

Originally published at https://medium.com/  on June 28, 2023.

Please follow and like me: