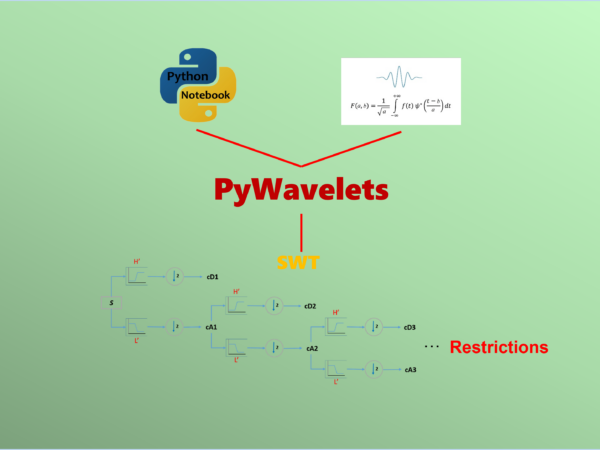
The main restrictions and requirements associated with SWT are important to ensure accurate and reliable results
Stationary Wavelet Transform (SWT) is a widely used signal processing technique that offers various advantages in signal analysis. However, it is important to be aware of the main restrictions and requirements associated with SWT to ensure accurate and reliable results. In this tutorial, we will explore two crucial restrictions of SWT: the signal length must be even and the signal length should be divisible by 2^n, where n represents the maximum number of decomposition levels.
1. The main restriction
1.1 Even Signal Length:
One of the primary restrictions of SWT is that the length of the signal being analyzed must be even. This requirement arises due to the filter bank structure used in the SWT algorithm. The filter banks operate by splitting the signal into even and odd samples, and the subsequent decomposition and reconstruction steps rely on maintaining this parity. If the signal length is odd, it must be padded with an additional sample to make it even before applying SWT.
1.2 Divisibility by 2^𝑛
Another important restriction is that the signal length should be divisible by 2^n, where n represents the number of desired decomposition levels. This requirement ensures the proper functioning of the SWT algorithm and allows for the consistent downsampling and filtering operations at each level. If the signal length does not meet this criterion, it may lead to incorrect decomposition results and potential loss of information.
2. Handling Restrictions:
To overcome these restrictions, the following steps can be taken:
2.1 Signal Length Adjustment
If the signal length is odd, it should be padded with an extra sample to make it even before applying SWT. This can be achieved by duplicating the last sample or using interpolation techniques to estimate the additional sample value.
2.2 Signal Length Modification
If the signal length is not divisible by 2^𝑛, it may be necessary to adjust the signal length by truncation or zero-padding. Truncation involves removing a few samples from the signal to make it divisible, while zero-padding involves adding zeros at the end of the signal to achieve the desired length.
It is important to note that modifying the signal length may introduce some artifacts or affect the analysis, particularly in the higher frequency bands. Therefore, careful consideration should be given to the choice and implementation of these adjustments.
3. Examples
Let’s consider a simple example to illustrate the restrictions of Stationary Wavelet Transform (SWT) regarding the signal length.
3.1 Even Signal Length
The first restriction of SWT is that the signal length must be even. In this case, the signal length is odd (17 samples).
import pywt
odd_S = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]
coeffs = pywt.swt(odd_S, 'db2', level=4)
coeffs
When we decompose the odd signal, there is ValueError. To satisfy the even length requirement, we need to pad the signal with an additional sample.
pad_S = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,17]
coeffs = pywt.swt(pad_S, 'db2')
coeffs[(array([ 9.106945 , 2.31078903, 3.7250026 , 5.13921616, 6.55342972,
7.96764328, 9.38185685, 10.79607041, 12.21028397, 13.62449753,
15.0387111 , 16.45292466, 17.86713822, 19.28135178, 20.69556535,
22.23918843, 25.62922001, 22.39647151]),
array([-2.19996188e+00, 1.66533454e-16, 1.11022302e-16, 3.33066907e-16,
4.44089210e-16, 2.22044605e-16, 0.00000000e+00, 2.22044605e-16,
1.33226763e-15, 4.44089210e-16, 8.88178420e-16, 8.88178420e-16,
4.44089210e-16, 4.44089210e-16, 8.88178420e-16, 4.82962913e-01,
7.85681613e+00, -6.13981716e+00]))]Now, we have an even-length signal of 18 samples, satisfying the requirement.
3.2 Divisibility by 2^𝑛
The second restriction is that the signal length should be divisible by 2^𝑛, where 𝑛 represents the maximum number of desired decomposition levels. Samples shoud be 2¹, 2², 2³,…, 2^n.pywt.swt_max_level(len(odd_S))

It shows that no levels of stationary wavelet decomposition are possible, and the signal to be transformed must have a size that is a multiple of 2^n for an n-level decomposition.
pywt.swt_max_level(len(pad_S))1
The above padded signal is even, but its maximum level is only 1. As we know in the previous article, a signle with 16 samples can decomposed into 4 levels.
pywt.swt_max_level(16)4
Let’s assume we want to decompose the signal into 4 levels or 5 levels, we need to modify the signal length by truncation or zero-padding to meet the requirement. For example, let’s truncate the signal by removing one sample to decompose the signal into 4 levels.
trunc_S = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]
coeffs = pywt.swt(trunc_S, 'db2')
coeffs[(array([34., 34., 34., 34., 34., 34., 34., 34., 34., 34., 34., 34., 34.,
34., 34., 34.]),
array([ -5. , 0.56217783, 5.02627944, 8.75833025,
12.12435565, 13.75833025, 14.02627944, 11.56217783,
5. , -0.56217783, -5.02627944, -8.75833025,
-12.12435565, -13.75833025, -14.02627944, -11.56217783])),
(array([27.57716447, 23.64411081, 20.48751428, 17.84855585, 15.46841646,
14.31302194, 14.12355325, 15.86593621, 20.50609665, 24.43915031,
27.59574684, 30.23470527, 32.61484466, 33.77023918, 33.95970787,
32.21732491]),
array([ -8.5732141 , -6.76148078, -5.01909782, -3.79435295,
-3.53553391, -2.56960808, -1.34486321, 1.81173332,
8.5732141 , 12.69573645, 14.81705679, 12.55703574,
3.53553391, -3.36464759, -8.45309576, -10.57441611])),
(array([18.19615242, 12. , 7.53589838, 5.80384758, 7.80384758,
9.80384758, 11.80384758, 13.80384758, 15.80384758, 17.80384758,
19.53589838, 22. , 26.19615242, 28.39230485, 29.12435565,
26.39230485]),
array([-4.92820323e+00, -2.73205081e+00, -1.00000000e+00, 7.21644966e-16,
-5.55111512e-17, -2.22044605e-16, 9.99200722e-16, 1.11022302e-15,
-1.77635684e-15, -6.66133815e-16, -1.00000000e+00, 7.32050808e-01,
8.92820323e+00, 9.66025404e+00, -2.00000000e+00, -7.66025404e+00])),
(array([ 8.62398208, 2.31078903, 3.7250026 , 5.13921616, 6.55342972,
7.96764328, 9.38185685, 10.79607041, 12.21028397, 13.62449753,
15.0387111 , 16.45292466, 17.86713822, 19.28135178, 22.76611771,
20.59402938]),
array([-2.07055236e+00, 1.66533454e-16, 1.11022302e-16, 3.33066907e-16,
4.44089210e-16, 2.22044605e-16, 0.00000000e+00, 2.22044605e-16,
1.33226763e-15, 4.44089210e-16, 8.88178420e-16, 8.88178420e-16,
4.44089210e-16, 4.44089210e-16, 7.72740661e+00, -5.65685425e+00]))]Conclusion
In this example, we demonstrated the restrictions of SWT regarding signal length. The signal length must be even, requiring padding with an additional sample if necessary. Additionally, the signal length should be divisible by 2^n to ensure proper decomposition, which may involve truncating or zero-padding the signal. By satisfying these restrictions, we can perform SWT accurately and obtain reliable results in signal analysis and processing. In this article, we just display the restrictions and general solutions to modify the signal length by truncation or zero-padding to meet the requirement. In the next article, we will show different methods to pad the signal in details.
Originally published at https://medium.com/ on June 28, 2023.