Wavelet transform can be used for noise removal, detection of abrupt discontinuities, and many more
Wavelet Transforms (WT) or wavelet analysis is probably the most recent solution to overcome the shortcomings of the Fourier Transform (FT). WT transforms a signal in period (or frequency) without losing time resolution. In the signal processing context, WT provides a method to decompose an input signal of interest into a set of elementary waveforms, i.e. “wavelets”., and then analyze the signal by examining the coefficients (or weights) of these wavelets. In this post, we will introduce where the wavelet transforms can be used.
1. Wavelet Transform Applications
In general, wavelets transforms can be used for stationary and nonstationary signals, including but not limited to the following:
- noise removal from the signals
- trend analysis and forecasting
- detection of abrupt discontinuities, change, or abnormal behavior, etc.
- compression of large amounts of data
- data encryption, i.e. secure the data
- Combine it with machine learning to improve the modelling accuracy
2. Some Examples
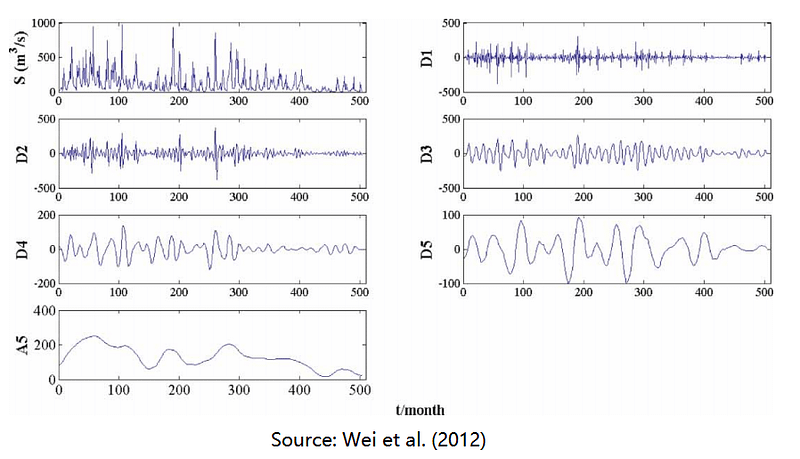
(1) Noise removal and trend analysis
A very good example of using wavelet transform for noise removal is one of my paper [1]. We use approximation instead of the original signal for modelling (or machine learning) because the original data is noisy. For example, we use the approximation (the red line) to replace the original by removing the high frequency signals (or noise).

(2) Abrupt discontinuities, and abnormal changes
For the following example, we can use wavelet transform to find abrupt discontinuities and abnormal changes.

(3) Increase Model Accuracy
I also published 3 paper about how to model the approximation and details separately, and then predict the approximation and detail(s) . Finally, we can obtain the prediction of the original by reconstructing predictions of the approximation and detail(s).
(4) Image Compression
Another example is applying wavelet transforms for big data or image compression. The new image compression standard called JPEG2000 is fully based on wavelets. From the following example, it illustrates that the image (my photo) is compressed by more than half. The original image is 32.5 Kb, while the compressed on using wavelet transforms has only 15.1Kb.

3. Online Course
If you are interested in learning Practical Wavelet Transforms from the very beginning, welcome to the courses via the following linage:
(1) Very basic one
(2) For Real-world projects
References:
Yuan, M., Wei, S., Sun, M., & Zhao, J. (2022). Wavelet Decomposition and Seq2Seq Hybrid Models for Water Quality Prediction. Water Resources, 49(4), 743–752.
Wei, Shouke, Depeng Zuo, and Jinxi Song. “Improving prediction accuracy of river discharge time series using a Wavelet-NAR artificial neural network.” Journal of Hydroinformatics 14, no. 4 (2012): 974–991.