Demonstrates how to easily implement DBSCAN clustering in Python using a real-world example
In the previous articles, we have demonstrated how to implement K-Means Clustering and Hierarchical Clustering, which are two popular unsupervised machine learning algorithms. We will continue to talk about another popular clusting algorithm- DBSCAN in this article.
DBSCAN (Density-Based Spatial Clustering of Applications with Noise) is a clustering algorithm that is widely used for unsupervised machine learning tasks, especially in situations where the data may have arbitrary shapes or sizes. Practical applications of DBSCAN include:
- Customer segmentation: DBSCAN can be used to segment customers based on their purchasing behavior, allowing businesses to better target their marketing efforts.
- Image segmentation: DBSCAN can be used to segment images based on their pixel values, making it useful for tasks such as object detection and tracking.
- Anomaly detection: DBSCAN can be used to detect anomalies in data, such as fraudulent transactions or system failures.
- Environmental monitoring: DBSCAN can be used to identify patterns in environmental data, such as identifying clusters of polluted areas or tracking changes in wildlife populations.
- Network analysis: DBSCAN can be used to identify clusters of nodes in a network, such as identifying communities in a social network or detecting anomalies in network traffic.
In this tutorial, we will cover the following 6 aspects of DBSCAN:
- What is DBSCAN?
- How does DBSCAN work?
- Advantages and Disadvantages of DBSCAN
- Data Preprocessing
- How to implement DBSCAN in Python?
- Visualize the DBSCAN Results
1. What is DBSCAN?
DBSCAN is a density-based clustering algorithm that groups together points that are close to each other in high-density regions, and separates out points that are in low-density regions. It was first introduced by Martin Ester, Hans-Peter Kriegel, Jörg Sander, and Xiaowei Xu in 1996.
The algorithm works by defining a “core” point as one that has at least a certain number of neighboring points within a specified radius. Points that are close to a core point, but do not have enough neighbors to be considered a core point themselves, are considered “border” points. Points that are not close to any core or border points are considered “noise” points.
2. How does DBSCAN work?
DBSCAN works by defining two important parameters: the radius of the neighborhood around a point, and the minimum number of points required to be considered a “core” point. These parameters are usually denoted by ε and MinPts, respectively.
The algorithm then proceeds as follows:
- Select an arbitrary point in the dataset that has not been visited yet and mark it as visited.
- Find all points within distance ε of the selected point and add them to a cluster.
- If the selected point is a core point (i.e., it has at least MinPts neighbors), repeat steps 1 and 2 for each of its neighbors. Add all of these points to the same cluster as the selected point.
- If the selected point is a border point (i.e., it has fewer than MinPts neighbors), add it to the cluster of its nearest core point (if any).
- Repeat steps 1-4 for all unvisited points in the dataset until all points have been visited.
The result of the algorithm is a set of clusters, each containing a set of points that are close to each other in high-density regions.
3. Advantages and Disadvantages of DBSCAN
DBSCAN has several advantages over other clustering algorithms:
- It does not require specifying the number of clusters beforehand.
- It can handle clusters of arbitrary shape and size.
- It can identify noise points that do not belong to any cluster.
However, DBSCAN also has some disadvantages:
- It can be sensitive to the choice of parameters ε and MinPts.
- It can be slow on large datasets.
- It may not work well in datasets with varying densities.
4. Data Preprocessing
Before implementing DBSCAN, we have to preprocess the dataset first.
4.1 Read data
We will use ‘Wholesale customers Data Set’ in UCI Machine learning Repository, which contains the annual spending in monetary units (m.u.) on diverse product categories. The dataset includes 440 customers with 8 attributes for each of these customers.
You can download it and load from your computer. But here, we will load it directly from the data link using pandas.
# import pandas
import pandas as pd
# read data from UCI Machine learning Repository
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/00292/Wholesale%20customers%20data.csv'
df = pd.read_csv(url)
df.head()
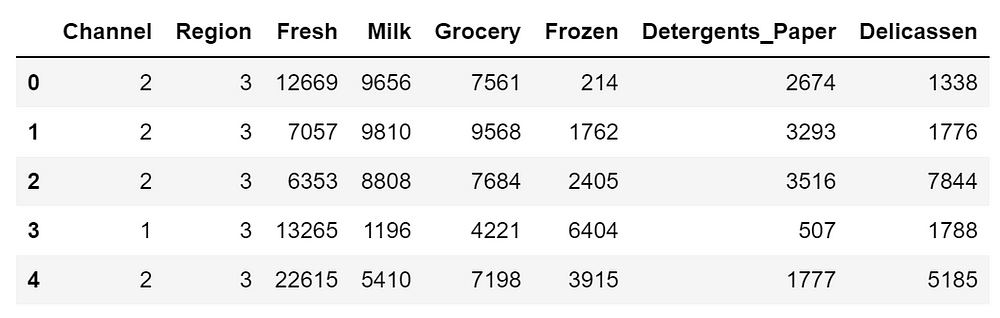
where:
- FRESH: annual spending (m.u.) on fresh products (Continuous);
- MILK: annual spending (m.u.) on milk products (Continuous);
- GROCERY: annual spending (m.u.)on grocery products (Continuous);
- FROZEN: annual spending (m.u.)on frozen products (Continuous)
- DETERGENTS_PAPER: annual spending (m.u.) on detergents and paper products (Continuous)
- DELICATESSEN: annual spending (m.u.)on and delicatessen products (Continuous);
- CHANNEL: customers’ Channel – Horeca (Hotel/Restaurant/Café) or Retail channel (Nominal)
- REGION: customers’ Region – Lisnon, Oporto or Other (Nominal)
4.2 Explore the dataset
In this section, we will explore the basic information of the data to detect if there are missing values and extreme values or outliers.
df.info()<class 'pandas.core.frame.DataFrame'> RangeIndex: 440 entries, 0 to 439 Data columns (total 8 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 Channel 440 non-null int64 1 Region 440 non-null int64 2 Fresh 440 non-null int64 3 Milk 440 non-null int64 4 Grocery 440 non-null int64 5 Frozen 440 non-null int64 6 Detergents_Paper 440 non-null int64 7 Delicassen 440 non-null int64 dtypes: int64(8) memory usage: 27.6 KB
The above information shows that there is no missing value in the dataset and all the data has 440 values with types of integer.
df.describe()
| Channel | Region | Fresh | Milk | Grocery | Frozen | Detergents_Paper | Delicassen | |
|---|---|---|---|---|---|---|---|---|
| count | 440.000000 | 440.000000 | 440.000000 | 440.000000 | 440.000000 | 440.000000 | 440.000000 | 440.000000 |
| mean | 1.322727 | 2.543182 | 12000.297727 | 5796.265909 | 7951.277273 | 3071.931818 | 2881.493182 | 1524.870455 |
| std | 0.468052 | 0.774272 | 12647.328865 | 7380.377175 | 9503.162829 | 4854.673333 | 4767.854448 | 2820.105937 |
| min | 1.000000 | 1.000000 | 3.000000 | 55.000000 | 3.000000 | 25.000000 | 3.000000 | 3.000000 |
| 25% | 1.000000 | 2.000000 | 3127.750000 | 1533.000000 | 2153.000000 | 742.250000 | 256.750000 | 408.250000 |
| 50% | 1.000000 | 3.000000 | 8504.000000 | 3627.000000 | 4755.500000 | 1526.000000 | 816.500000 | 965.500000 |
| 75% | 2.000000 | 3.000000 | 16933.750000 | 7190.250000 | 10655.750000 | 3554.250000 | 3922.000000 | 1820.250000 |
| max | 2.000000 | 3.000000 | 112151.000000 | 73498.000000 | 92780.000000 | 60869.000000 | 40827.000000 | 47943.000000 |
The descriptive statistics display that all the variables are continuous except for ‘Channel’ and ‘Region’.
4.3 Select features
We select all the features except ‘Channel’ and ‘Region’ for clustering, thus we drop them using pandas drop() method.
features = df.drop(['Channel','Region'],axis=1)
features.head()
| Fresh | Milk | Grocery | Frozen | Detergents_Paper | Delicassen | |
|---|---|---|---|---|---|---|
| 0 | 12669 | 9656 | 7561 | 214 | 2674 | 1338 |
| 1 | 7057 | 9810 | 9568 | 1762 | 3293 | 1776 |
| 2 | 6353 | 8808 | 7684 | 2405 | 3516 | 7844 |
| 3 | 13265 | 1196 | 4221 | 6404 | 507 | 1788 |
| 4 | 22615 | 5410 | 7198 | 3915 | 1777 | 5185 |
4.4 Visualize the data
We visualize the data roughly to see its general patterns, and we will use pandas, matplotlib and ‘ggplot’ style for the plots.
import matplotlib.pyplot as plt
# set the plotting style to 'ggplot'
plt.style.use('ggplot')
# use pandas to create a box plot
features.plot.box(rot=45)
<Axes: >
The box plot demonstrate that there are extreme values or outliers in the dataset. Let’s select two variables, say ‘Fresh’ and ‘Milk’ to visualize their patterns in details.
plt.scatter(features.Fresh, features.Milk, s=35, alpha=0.9)
plt.xlabel('Fresh (m.u.)')
plt.ylabel('Milk (m.u.)')
Text(0, 0.5, 'Milk (m.u.)')
From the above result, it is seen that there are two clear clusters: the normal one and outliers.
4.5 Normalize/Standardize features
Standardizing the data ensures that all features are on the same scale and have the same influence on the clustering algorithm. We use StandardScaler() function in scikit-learn to standardize the selected features.
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X = scaler.fit_transform(features)
X
array([[ 0.05293319, 0.52356777, -0.04111489, -0.58936716, -0.04356873,
-0.06633906],
[-0.39130197, 0.54445767, 0.17031835, -0.27013618, 0.08640684,
0.08915105],
[-0.44702926, 0.40853771, -0.0281571 , -0.13753572, 0.13323164,
2.24329255],
...,
[ 0.20032554, 1.31467078, 2.34838631, -0.54337975, 2.51121768,
0.12145607],
[-0.13538389, -0.51753572, -0.60251388, -0.41944059, -0.56977032,
0.21304614],
[-0.72930698, -0.5559243 , -0.57322717, -0.62009417, -0.50488752,
-0.52286938]])5. How to implement DBSCAN in Python
DBSCAN is implemented in several popular machine learning libraries, including scikit-learn and PyTorch. In this section, we will show how to implement DBSCAN in scikit-learn.
5.1 Rule of Specifing MinPoints and Epsilon
Specifying the values for MinPts and ε can be challenging, as they can greatly affect the results of the clustering. Here are some general guidelines for choosing these parameters:
ε: The value of ε determines the radius of the neighborhood around each point. Points within this radius are considered as part of the same cluster. A larger ε will result in fewer clusters, while a smaller ε will result in more clusters. One way to determine the appropriate value of ε is to use a k-distance plot, which plots the distance to the k-th nearest neighbor for each point in the dataset. The value of ε can be chosen as the distance corresponding to a knee or elbow point in the plot.
MinPts: The value of MinPts determines the minimum number of points required for a cluster to be formed. A larger MinPts will result in fewer clusters, while a smaller MinPts will result in more clusters. A common rule of thumb is to set MinPts equal to the dimensionality of the dataset plus one (i.e., MinPts = d + 1), where d is the number of dimensions in the dataset. The second common rule of thumb for setting the value is that if the dataset has two dimensions, the minimum number of points required to form a cluster (i.e., min_samples) should be set to 4. If the dataset has more than two dimensions, the minimum number of points required to form a cluster should be set to twice the number of dimensions in the dataset (i.e., min_samples = 2 * d).
It’s important to note that the optimal values of ε and MinPts can vary depending on the characteristics of the dataset and the desired level of granularity in the clustering. In practice, it may be necessary to experiment with different values of these parameters and evaluate the quality of the resulting clusters using metrics such as silhouette score or visual inspection.
5.2 Determine the knee point
Based on the above rule, the knee point can be used to determine the optimal value of the epsilon parameter (ε).
Step 1: Compute the distance matrix using the NearestNeighbors algorithm
In this process, we first use the NearestNeighbors algorithm to compute the pairwise distances between all points in the data matrix X.
from sklearn.neighbors import NearestNeighbors
neigh = NearestNeighbors(n_neighbors=2)
nbrs = neigh.fit(X)
distances, indices = nbrs.kneighbors(X)
Step 2: Plot the distances in ascending order
Then, we sort the distances in ascending order using sort method of NumPy and plot them using Matplotlib.
import numpy as np
distances = np.sort(distances[:,1])
plt.plot(distances)
[<matplotlib.lines.Line2D at 0x1e05fd9ee50>]
Step 3: Use the KneeLocator to determine the elbow point in the curve
First, we install the Kneed package, which provides an automated method for determining the knee point, or the optimal value of a parameter, in a curve. The package implements a variation of the “knee finding” algorithm that works by detecting the point of maximum curvature in a curve. You can install it using pip or conda.
pip install kneed
or
conda install -c conda-forge kneed
Retrieving notices: ...working... done
Collecting package metadata (current_repodata.json): ...working... done
Solving environment: ...working... done
## Package Plan ##
environment location: C:\Users\shouk\anaconda3
added / updated specs:
- kneed
The following packages will be downloaded:
package | build
---------------------------|-----------------
kneed-0.7.0 | pyh9f0ad1d_0 12 KB conda-forge
------------------------------------------------------------
Total: 12 KB
The following NEW packages will be INSTALLED:
kneed conda-forge/noarch::kneed-0.7.0-pyh9f0ad1d_0
Downloading and Extracting Packages
kneed-0.7.0 | 12 KB | | 0%
kneed-0.7.0 | 12 KB | ########## | 100%
kneed-0.7.0 | 12 KB | ########## | 100%
Preparing transaction: ...working... done
Verifying transaction: ...working... done
Executing transaction: ...working... done
Note: you may need to restart the kernel to use updated packages.
Step 4: Find the elbow point in the curve
Finally, we use the KneeLocator function from the kneed package to find the elbow point in the curve, which corresponds to the optimal value of epsilon for DBSCAN clustering.
The S parameter controls the sensitivity of the algorithm to detect elbows, and the curve and direction parameters specify the type and direction of the curve, respectively. The optimal value of epsilon is printed to the console.
from kneed import KneeLocator
kneedle = KneeLocator(range(len(distances)), distances, S=1.0, curve="convex", direction="increasing")
optimal_epsilon = distances[kneedle.knee]
print("Optimal epsilon: ", optimal_epsilon)
Optimal epsilon: 1.6070889053161401
You can also plot the diagram easily using kneedle.plot_knee() method of the package.
kneedle.plot_knee()
plt.show()
5.3 Determine MinPts
We use the second common rule of thumb for setting the value of MinPts. This rule is based on the observation that as the dimensionality of the data increases, the density of the data decreases, and it becomes more difficult to identify meaningful clusters. By setting min_samples to a higher value in high-dimensional datasets, we can ensure that the resulting clusters are more robust and have a higher level of statistical significance.
d = 6
min_samples = 2*d
5.4 Apply DBSCAN to cluster the data
Then DBSCAN method will be applied to cluster the data based on the selected features. In this example, we have set ε=1.6 and MinPts=12.
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=1.6, min_samples=min_samples).fit(X)
We then call the dbscan.labels_ or fit_predict method of the DBSCAN to print the cluster labels.
labels = dbscan.labels_ # or
# labels = dbscan.fit_predict(X)
labels
array([ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, -1, 0, 0, 0,
0, 0, 0, 0, 0, -1, 0, 0, 0, 0, -1, 0, 0, 0, -1, 0, 0,
0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
-1, -1, -1, 0, 0, 0, 0, -1, -1, 0, 0, 0, 0, 0, 0, 0, 0,
0, -1, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, -1, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, -1, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, -1, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0],
dtype=int64)Let’s calculate the number of clusters in labels.
# Number of clusters in labels, ignoring noise if present.
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
n_noise_ = list(labels).count(-1)
print("Estimated number of clusters: %d" % n_clusters_)
print("Estimated number of noise points: %d" % n_noise_)
Estimated number of clusters: 1 Estimated number of noise points: 30
Now, we evaluate the cluster result with silhouette_score.
from sklearn import metrics
print(f"Silhouette Coefficient: {metrics.silhouette_score(X, labels):.3f}")
Silhouette Coefficient: 0.646
6. Visualize the Results
6.1 Visualize clustering results with scatter matrix plot
First, we add the cluster labels on the result DateFrame.
# add the cluster labels on the result DateFrame
results = features.copy()
results['Clusters'] = dbscan.labels_
results.head()
| Fresh | Milk | Grocery | Frozen | Detergents_Paper | Delicassen | Clusters | |
|---|---|---|---|---|---|---|---|
| 0 | 12669 | 9656 | 7561 | 214 | 2674 | 1338 | 0 |
| 1 | 7057 | 9810 | 9568 | 1762 | 3293 | 1776 | 0 |
| 2 | 6353 | 8808 | 7684 | 2405 | 3516 | 7844 | 0 |
| 3 | 13265 | 1196 | 4221 | 6404 | 507 | 1788 | 0 |
| 4 | 22615 | 5410 | 7198 | 3915 | 1777 | 5185 | 0 |
6.2 Visualize clustering results with scatter matrix plot
We can visualize the results of the clustering by different plots, for example, scatter matrix with the points colored based on their clusters.
import seaborn as sns
# Create a scatterplot matrix
sns.pairplot(results, hue='Clusters', palette='Dark2')
<seaborn.axisgrid.PairGrid at 0x1e0693e4be0>
As we can see, DBSCAN has successfully identified two clusters in the data, which correspond to different segments of customers based on their spending behavior. These segments can be used by wholesalers to target their marketing and promotions towards specific groups of customers.
6.3 Parallel coordinate plot
We can create a parallel coordinate plot to have further insights on the data.
plt.figure(figsize=(15,8))
pd.plotting.parallel_coordinates(results,'Clusters',alpha=0.90)
plt.xticks(rotation=45)
plt.show()
The above plot displays that the spending on each product of cluster -1, i.e. the anomaly group with extreme values (outliers) in the data is much higher than that of the normal customers.
6.4 Average results
We investigate the results by averaging the spending on each product.
results_mean = results.groupby(['Clusters']).mean()
results_mean.reset_index(inplace=True)
results_mean
| Clusters | Fresh | Milk | Grocery | Frozen | Detergents_Paper | Delicassen | |
|---|---|---|---|---|---|---|---|
| 0 | -1 | 25096.066667 | 22697.600000 | 26748.900000 | 9739.500000 | 10293.533333 | 6083.100000 |
| 1 | 0 | 11042.070732 | 4559.582927 | 6575.841463 | 2584.060976 | 2339.148780 | 1191.341463 |
We can also create a parallel coordinate plot for the average spending of each cluster.
plt.figure(figsize=(15,8))
pd.plotting.parallel_coordinates(results_mean,'Clusters',alpha=0.9,sort_labels=True)
plt.xticks(rotation=80)
plt.show()
The above result clearly that the spending on each produces in the anomaly cluster (-1) is over 2~5 time higher than the normal group (0). Therefore, wholesalers should pay more attention to this group.
Conclusions
DBSCAN is a powerful clustering algorithm that can identify clusters of arbitrary shapes and sizes in a dataset, without requiring the number of clusters to be specified in advance. It also has the ability to identify noise points that do not belong to any cluster, or belongs to anomaly cluster in our case. DBSCAN is widely used in various domains, including computer vision, image segmentation, anomaly detection, and customer segmentation.
Overall, DBSCAN is a versatile clustering algorithm that can be used in many different domains to identify patterns and structures in data.